用swift手工撸一个最大堆排序和最小堆排序
2016-03-23 小文字
前言
自打apple出了swift,iOS开发又变得波涛汹涌,笔者也陆续自学了Swift1.x/2.x, 正所谓纸上得来终觉浅,今天正好那swift来写一下堆排序算法,既巩固语法知识,也重温经典算法的实现思路。
什么是堆,堆排序,最大堆,最小堆… ?
科班出身的我们一般知道堆排序(认不认识就不一定了–!), 这里谈的堆是数据结构的一种,首先堆是树,是二叉树,接近完美二叉树,不同处在于其叶子节点可以不是满的,另外就是要满足堆的性质:
1.最大堆:叶子节点都小于等于起父节点
2.最小堆:叶子节点都大于等于父节点
看张图就一下子明白了
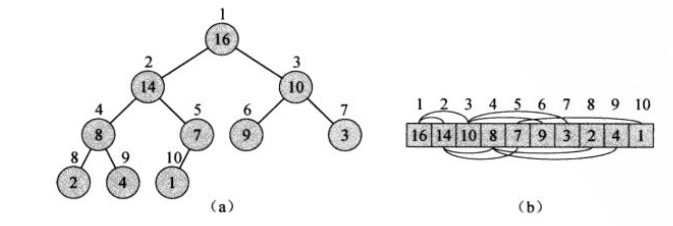
那么基于堆结构进行排序操作,自然就是堆排序了,一般在算法介绍和实现中,我们都是利用一维数组实现原址排序;
堆排序思路
现在重温一下,这个经典的堆排序是怎么实现的。
以算法导论中对堆排序的介绍,可以简单的归结为三句话:
- 维持堆的性质
- 构建堆
- 堆排序

维持堆的性质
我们以最大堆来介绍(后续会分别给出最大堆和最小堆的实现).所谓维持堆得性质就是字面意思,也就是确保叶子节点和父节点的关系是堆得关系; 那么怎么维持呢?
这里我们是以某一个节点为起始点,调整其自身与子节点的关系,使得父节点总是大于子节点,处理完毕后递归操作调整后的节点;
我们来看一下具体的实现:
/**
* 维护最大堆的性质
*/
func heapify(inout A:[Int], i:Int, size:Int) {
var l = 2 * i
var r = l + 1
var largest = i
if l < size && A[l] > A[i] {
largest = l
}
if r < size && A[r] > A[largest] {
largest = r
}
if largest != i {
swap(&A, i, largest)
heapify(&A, largest, size)
}
}有效代码也就10行上下, 简单解释下,根据传入的节点在数组内的索引,计算出左右子节点,然后比较比较子节点的值大小,将大的值对调为父节点的值,最后递归处理新节点;
构建堆
现在来看第二步,也就是构建一个堆。我们的输入数据源是一个以为数组,需要通过构建,将其以堆的性质加以调整; 我们来看一下具体的实现:
/**
* 构建最大堆
*/
func buildHeap(inout A:[Int]) {
for var i = A.count/2; i >= 0; i-- {
heapify(&A, i, A.count)
}
println("build heap:\(A)")
}简单解释下,根据上一步已经得到的维护堆性质的函数,我们队数组内的所有非叶子节点遍历,针对每个节点都做一遍堆处理,最后得到的就是一个完整的堆;
可能不理解的骚年会问了,为什么数组遍历不是全量的,而是[A.count/2, 0]?
这个问题,我想最好的的答案是你画一个二叉树,一眼就能明白,这棵树中非叶子节点的索引就是count/2;
堆排序
终于到了见证奇迹的时刻,我们把数组排个序输出一下。
/**
*堆排序
*/
func heapSort(inout A:[Int]) {
buildHeap(&A)
var size = A.count
for var i = A.count - 1; i >= 1; i-- {
swap(&A, i, 0)
size--
heapify(&A, 0, size)
}
println("sorted heap:\(A)")
}这里呢,需要注意的地方就是每次得到最大值后,我们需要把问题的解规模减小,因为我们是原址排序,实际上是把一维数组分为了未排序的堆和已排序的数组两部分,已排序的部分放在数组尾部;
验证一下
随便搞个数组,我们排个队
var A = [4, 1, 3, 2, 16, 9,9, 10, 14, 8, 7]
heapSort(&A)avens-MacBook-Pro:aven$ ./max-heap-sort.swift
build heap:[16, 14, 9, 10, 8, 7, 9, 2, 3, 1, 4]
sorted heap:[1, 2, 3, 4, 7, 8, 9, 9, 10, 14, 16]小结
上面我们已经完成了最大堆的算法的编码,最小堆也是类似的,下面是完整的最小堆排序和最大最排序; 算法这东西如果能理解的话写起来就不太难,所以一定要对理论有所了解,真正理解了算法思路才能吧思路写成代码。
完整代码:
最大堆排序:max-heap-sort.swift 最小堆排序:min-heap-sort.swift