小文字 吃饭，睡觉，遛狗头

新瓶装老酒--快速排序|随机快速排序

2016-03-27 小文字

img

前言

接上，本文讲的是排序里的快排算法实现。

思路分析

照例还是先理解快排，了解常规实现的思路。

快速排序作为比较排序的一种，包含了归并，插入的两种特性。 具体来讲，快排会不断细分问题的规模，这一点类似归并中问题的拆解；同时在确定分解边界的时候运用的是遍历比较，这与插入排序中选定分割线很像；

下面看一下具体的操作步骤：

1. 拆分数组，确定分割主元，使得主元的取值恰好大于左侧所有值，小于右侧所有值；
2. 根据主原下标，递归求解被划分的数组区域；

分组

分组过程的起始点是假设以数组末尾的元素为第一个主元（当然可以通过预处理使用非末尾元素作为主元，在后续的随机快排中会单独介绍），现在我们要把数组扫描一遍，在遍历的过程中 我们把每个元素和主元作比较，把小于主元的放在一个区域，大于主元的放在另一个区域，这么一来，实际上在不断的遍历过程中会产生三个数据区域，两个辅助索引：

1.小于主元的存放区域
2.大于主元的存放区域
3.尚未比较的原数据区域

由于我们是原址排序，也就是在原数组内通过下标区域直接划分上述的三个数据区域，这里就会需要区域的边界索引，也就是引入了2个辅助索引； 在个分组函数中，入参是数组指针，数据区域的在数组内的首尾下标；将代码实现与上述区域结合起来的话，他们之间的关系是这样的：

1.小于主元=》[p, i]
2.大于主元=》[i+1, j-1]
3.尚未比较=》[j, r-1]

img

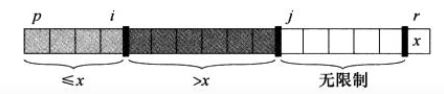
可以记住这张图，看着图比较好理解分组的操作流程；

下面是分组的实现：

/**
* 扫描数组进行分组，确定分组分割下标
*/
func partition(inout A:[Int], p:Int, r:Int) -> Int{
    var x = A[r]
    var i = p - 1
    for var j = p; j < r; j++ {
        if A[j] <= x {
            i++
            swap(&A, i, j)
        }
    }
    swap(&A, ++i, r)
    return i
}

排序

实际上，在快排内，最重要的就是分组实现区域内的重排序，有了它，在主程序中只需恰当的递归处理即可；

/**
* 快排
*/
func quickSort(inout A:[Int], p:Int, r:Int) {
    if p < r {
        var q = partition(&A, p, r)
        quickSort(&A, p, q - 1 )
        quickSort(&A, q + 1, r)
    }
}

最后我们补一个测试数组，看看效果

var A = [2, 8, 7, 1, 3, 5, 6, 4]
println("Array:\(A)")
quickSort(&A, 0, A.count - 1)

输出

avens-MacBook-Pro: aven$ ./quick-sort.swift 
Array:[2, 8, 7, 1, 3, 5, 6, 4]
Sorted:[1, 2, 3, 4, 5, 6, 7, 8]

随机快速排序

现在在看一下随机快排，在算法导论中有大量的性能，空间复杂度，时间复杂度的考量与证明，随机快排就是为了避免快排的最坏情况而来的； 大多数算法在最坏情况下的复杂度都是相对比较差的，在时间生活中快排的性能一般接近于最优，但是也有很低概率出现最坏情况：

最坏情况是每次的分组操作都恰好有一个区域大小是0，也就是划分的整理遍历操作没有实质上的实现对半的重排；

因此，在选择起始主元的时候，我们可以在数组内随机取一个下标的元素和最后的元素交换，那么这样一来，每个元素作为初始主元的概率都是一样的，也就避免了数组本身排序特性导致快排出现最后情况；

小结

排序中的边界处理往往容易出问题，特别是涉及递归的操作中，需要仔细理解，调整算法，特别是算法导论中基本都是思路原理介绍很详尽，唯一要注意的的数组其实下标这些细节；

完整代码：

快速排序：quick-sort.swift 快速排序：randomized-quick-sort.swift

Related Posts